
Interpréter les données de vraie vie à travers deux exemples concrets
Si les études randomisées forment la base de la médecine fondée sur les preuves, les études d’observation (« études de vraie vie », « études du monde réel ») apportent des enseignements qui en sont complémentaires. Lorsqu’elles sont représentatives d’une population (« population-based » studies), elles fournissent des données épidémiologiques qui sont essentielles pour connaître l’évolution des maladies, les populations qu’elles frappent, leur prise en charge et leur pronostic. Ces études épidémiologiques sont alors essentiellement descriptives et leur interprétation ne pose guère de problème : les chiffres sont les chiffres !
Il en va tout autrement quand on veut utiliser ces données d’observation pour tirer des enseignements sur l’efficacité ou le risque d’un traitement, qu’il soit médicamenteux ou d’autre nature.
Dans la « vraie vie », un traitement n’est pas utilisé au hasard
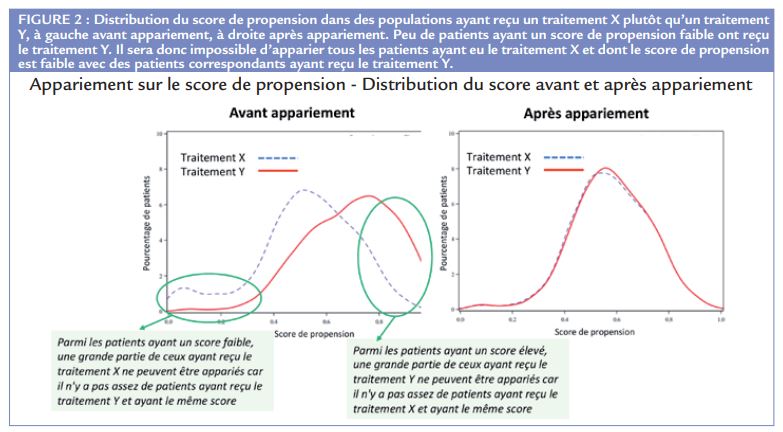
L’écueil fondamental, pour étudier le rôle d’un traitement, est que dans des conditions d’utilisation réelle, le traitement n’est pas prescrit au hasard : il est employé, de préférence à un autre, pour des raisons spécifiques, qui peuvent être liées à l’état du patient lui-même, mais aussi à des facteurs extérieurs, comme les choix personnels du médecin qui décide du traitement. Les biais induits peuvent être facilement illustrés par la Figure 1.

L’objectif de l’étude de vraie vie qui figure ici est de savoir si un traitement X permet d’éviter la survenue de crises cardiaques. On recueille donc les données d’un échantillon de 1 000 personnes, dont une moitié a reçu le traitement et l’autre pas. Au terme du suivi, on décompte 130 infarctus chez les patients qui ont reçu le traitement, contre 210 chez ceux qui n’ont pas été traités ; la différence est importante, témoignant d’une baisse de 38 % du risque d’infarctus chez les personnes traitées. A première vue, le traitement semble donc efficace, d’autant qu’un test statistique portant sur cette comparaison donnerait une valeur de P <0,001. Mais c’est sans compter sur les différences de caractéristiques entre les deux groupes ; en particulier, il y a 60 % de femmes dans le groupe traité, mais seulement 20 % dans le groupe non traité. Si l’on observe maintenant séparément le devenir des hommes et des femmes, il y a 100 événements pour 200 hommes traités et 200 événements pour 400 hommes non traités, soit une proportion de 50 % d’événements, chez les patients traités comme ceux non traités. Chez les femmes, il y a 30 événements chez les 300 qui ont été traitées (10 %) et 10 événements chez les 100 femmes qui n’ont pas reçu le traitement (10 % également). En fait, le traitement n’a aucun effet si l’on tient compte du sexe : les femmes ont été plus souvent traitées, mais elles ont à la base un risque de faire un infarctus qui est plus faible ; l’apparente efficacité du traitement est simplement liée au fait que les caractéristiques des personnes traités et non traitées diffèrent.
Les méthodes utilisées
pour « amortir » les inégalités de départ Il existe d’assez nombreuses techniques statistiques dont le but est « d’amortir » les différences entre les caractéristiques initiales des groupes que l’on souhaite comparer. Leur but est de tenter de déterminer si un traitement est efficace ou dangereux (ou plus efficace ou dangereux qu’un autre), toutes choses égales par ailleurs : en d’autres termes, le traitement serait-il plus ou moins efficace ou dangereux si les personnes traitées avaient exactement le même profil que les personnes non traitées
Les techniques d’analyse multivariée
Schématiquement, deux grandes techniques sont utilisées, qui répondent aux mêmes principes : la régression logistique binaire et la régression de Cox. La première est utilisée pour évaluer les événements sans tenir compte de la durée d’exposition ; c’est celle-ci qu’on emploie le plus souvent quand on veut évaluer l’effet d’un traitement sur la mortalité hospitalière. Les résultats sont exprimés en odds ratio (OR, rapport des cotes, en français) avec l’intervalle de confiance à 95 % correspondant. L’analyse de Cox, elle, est utilisée lorsque le suivi clinique est plus long, par exemple quand on veut connaitre le risque de survenue d’un événement dans l’année qui suit l’introduction du traitement ; les résultats s’expriment comme hazard ratio (HR, rapport de risque) avec l’intervalle de confiance correspondant. Si la survenue de l’événement étudié n’est pas homogène au fi l du temps (généralement, plus fréquente au début), on peut affiner la méthode de Cox en la rendant dépendante du temps ; on aura alors un hazard ratio pour la première période et un autre hazard ratio pour la seconde période. Mais ce sont là des finesses statistiques qui ne sont habituellement pas les plus fondamentales. L’intervalle de confiance est important à considérer, car il signifie que les résultats « vrais » ont 90 % de chances de se trouver à l’intérieur de cet intervalle ; concrètement, si l’on prend l’exemple de la comparaison apixaban-AVK sur le risque d’événements emboliques présenté ci-dessous, le HR est à 0,60, avec un intervalle de confiance entre 0,56 et 0,65 ; cela signifie qu’après ajustement, la réduction du risque embolique par rapport aux AVK dans la population étudiée a 90 % de chances de se situer entre 35 % et 44 %.
Le score de propension
La seconde méthode est apparue dans les publications médicales il y a une quinzaine d’années. Il s’agit de l’utilisation des scores de propension (« propensity scores »). Cette fois-ci, il s’agit de rechercher les caractéristiques qui vont conduire à la prescription d’un traitement donné : on utilise pour cela à nouveau une analyse multivariée qui permet d’attribuer à chaque patient une probabilité de recevoir le traitement, en fonction de ses caractéristiques (typiquement l’âge, le sexe, les facteurs de risque, les comorbidités et antécédents médicaux, les traitements co-prescrits etc…) ; c’est cette probabilité individuelle qu’on appelle le score de propension. Chaque patient étudié a donc un score de propension, qu’il ait effectivement reçu ou non le traitement. Le score peut ensuite être utilisé de trois manières pour juger de l’intérêt du traitement :
1) comme co-variable dans une analyse multivariée de Cox ; l’analyse utilise alors uniquement deux variables, le traitement à l’étude (utilisé oui ou non) et le score de propension, qui « résume » le profil des patients ;
2) pour construire des groupes de patients parmi la population étudiée, en fonction de n-tiles du score de propension ; par exemple, des quintiles, le quintile 1 représentant les 20 % de la population ayant le score le plus faible, le quintile 5 ceux ayant le score le plus élevé ; on regarde alors au sein de chaque quintile si le pronostic est meilleur ou moins bon avec le traitement étudié ; si les résultats sont concordants (par exemple, tous favorables) quel que soit le quintile de population, il y a de grandes chances que le traitement soit réellement efficace, car, quel que soit le profil des patients, il est associé à un meilleur pronostic ;
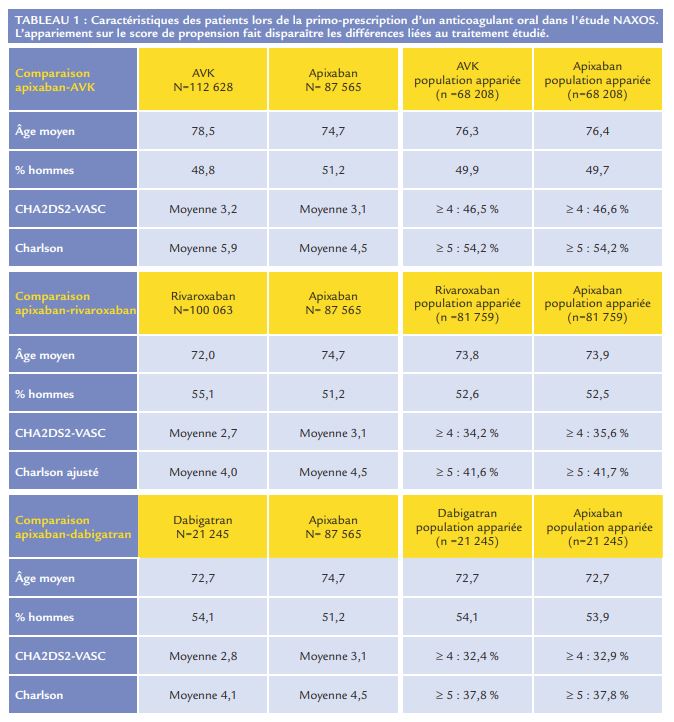
3) la troisième méthode est celle qui est le plus fréquemment employée ; il s’agit d’un appariement sur le score de propension : pour un patient ayant reçu le traitement et ayant un score de propension x, disons 0,63, on apparie un patient (ou parfois plus) qui n’a pas reçu le traitement, mais qui a également un score à 0,63. On construit alors deux cohortes, dont les caractéristiques au départ sont remarquablement similaires (Tableau 1, colonnes de droite). Parmi ces 3 façons d’utiliser le score de propension, les deux premières permettent de conserver l’ensemble de la population, tandis que la troisième laisse de côté des patients aux deux extrémités de la courbe de distribution du score (Figure 2), ce qui peut engendrer des problèmes de manque de puissance statistique.
En plus du score de propension « classique », il est possible de calculer des scores de propension dits « de haute dimension » (high-dimensional propensity scores), qui intègrent dans le calcul du score des variables a priori sans rapport avec l’objectif recherché (notamment des prescriptions médicamenteuses n’ayant aucun rapport avec la pathologie concernée, le lieu d’habitation, le type de couverture sociale, la réalisation d’examens biologiques, les actes diagnostiques ambulatoires etc…). L’idée qui sous-tend l’utilisation du score de haute dimension est qu’en intégrant des variables sans rapport avec l’objectif recherché, on est plus susceptible d’amortir d’éventuelles différences sur des variables ayant une importance pronostique mais qui ne seraient pas disponibles (par exemple, en cardiologie, une variable comme la fraction d’éjection du ventricule gauche n’est pas disponible dans les données actuelles du SNDS). L’utilisation des scores de propension de haute dimension se fait exactement de la même façon que celles des scores de propension « classiques ».
Un exemple d’utilisation des différentes méthodes statistiques pour la comparaison des traitements anticoagulants oraux tels qu’utilisés dans la vraie vie en France : l’étude NAXOS
La France dispose d’une ressource remarquable, la base SNDS, qui croise les données de remboursement des traitements et les données recueillies chez les patients hospitalisés. C’est cette base de données colossale qui a été utilisée pour répondre à la demande des autorités de santé qui souhaitaient vérifier les résultats observés « en vraie vie » avec l’utilisation de l’apixaban, comparée à celle des autres anticoagulants oraux disponibles en France, chez les malades ayant une fibrillation atriale non valvulaire.
L’étude a inclus tous les patients ayant une primoprescription d’un anticoagulant oral pour une fibrillation atriale non valvulaire, entre 2014 et 2016 en France. En tout, 112 628 patients ont eu un antivitamine K, 100 063 patients du rivaroxaban, 87 565 patients de l’apixaban et 21 245 patients du dabigatran. Le profil des patients différait sensiblement selon l’anticoagulant prescrit, avec un profil globalement plus sévère pour les AVK, intermédiaire pour l’apixaban, et moins sévère pour le dabigatran et le rivaroxaban (Tableau 1). L’étude s’est focalisée sur trois objectifs après un an de suivi : la sécurité (risque de saignement conduisant à une hospitalisation), l’efficacité (risque d’AVC ou d’embolie artérielle), et la mortalité globale. Quatre méthodes d’ajustement ont été utilisées, de façon à vérifier la cohérence des résultats : une analyse de populations appariées sur les scores de propension classiques (un score est calculé pour chaque comparaison : apixaban-AVK, apixaban-rivaroxaban, apixaban-dabigatran ; les cohortes comparatives sont construites à partir de ces scores) qui est l’analyse principale présentée dans la publication princeps1 ; une analyse de populations appariées sur le score de propension de haute dimension ; une analyse utilisant le score de propension comme co-variable dans un modèle multivarié classique ; une analyse fondée sur un modèle multivarié classique intégrant les traitements comparés et les autres variables pronostiques.
Dans les cohortes appariées sur le score de propension, les patients recevant de l’apixaban ont un profil identique à celui des patients recevant l’anticoagulant comparateur (Tableau 1).
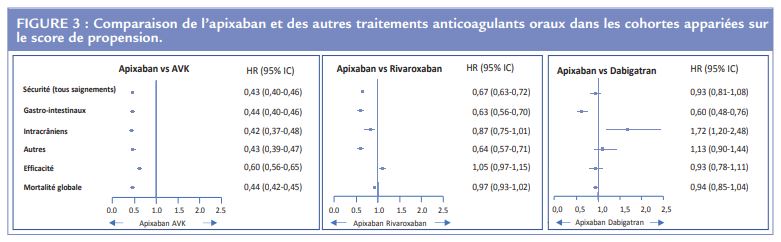
En termes de sécurité, d’efficacité et de mortalité, les résultats observés avec l’apixaban sont meilleurs que ceux constatés avec les AVK ; par rapport au rivaroxaban, les résultats sont meilleurs pour l’apixaban en termes de saignement, et comparables pour l’efficacité et la mortalité ; enfin, en comparaison du dabigatran les résultats sont comparables pour l’efficacité, la sécurité et la mortalité (Figure 3).
En comparaison du dabigatran, l’apixaban est associé à un moindre risque de saignement digestif, mais à un risque majoré de saignement intracrânien ; ces derniers événements sont rares, comme en témoigne l’étendue de l’écart-type correspondant. (Figure 3).
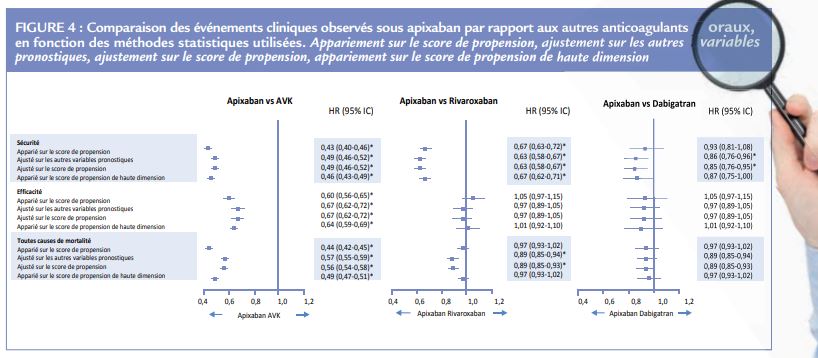
Dans l’ensemble les différentes approches statistiques ont donné des résultats très homogènes (Figure 4). C’est le cas notamment des comparaisons AVK-apixaban et dabigatran-apixaban. Pour la comparaison entre rivaroxaban et apixaban, les résultats sont homogènes pour ce qui est de la sécurité et de l’efficacité, mais discordants pour la mortalité globale : les deux analyses appariées (sur le score de propension et sur le score de propension de haute dimension) ne montrent pas de différence, tandis que l’analyse multivariée classique et celle ajustée sur le score de propension notent une mortalité plus faible sous apixaban. Il faut interpréter ces résultats discordants avec beaucoup de réserve : par essence, les analyses appariées n’incluent pas les patients pour lesquels l’appariement a été impossible (aux deux extrémités de la courbe de distribution du score) ce qui peut rendre compte en partie de la discordance ; inversement, des facteurs de confusion non reconnus peuvent également exister et venir entacher les résultats des analyses multivariées. En pratique, les conclusions des études d’observation ont plus de chances de refléter un effet réel quand les différentes méthodes d’ajustement statistique aboutissent à des résultats concordants.
L’importance de la méthodologie dans les études d’observation
En dehors des finesses statistiques, la méthodologie générale des études d’observation est capitale, comme elle peut l’être dans les études randomisées. On peut illustrer cela avec une étude qui a fait beaucoup parler d’elle au cours des derniers mois, celle qui a servi à « vendre » le concept de l’efficacité de l’hydroxychloroquine dans le traitement de la COVID-192.
Cette étude pose de nombreux problèmes méthodologiques. Le premier point est la dénomination-même de l’étude, présentée comme un essai non-randomisé ouvert. En réalité il s’agit d’une étude de cohorte (étude observationnelle), comparant des patients ayant été hospitalisés à l’IHU Méditerranée Infection de Marseille et traités par hydroxychloroquine, et des patients n’ayant pas reçu ce traitement et provenant de Marseille, Nice, Avignon et Briançon ; il n’est pas directement précisé si ces derniers patients étaient ou non hospitalisés au départ.
Le second point est le choix du critère destiné à évaluer l’efficacité d’un traitement. Dans l’étude en question, il ne s’agit pas d’un critère clinique (intubation, mortalité ou autre), mais d’un critère intermédiaire, la négativation du test PCR pour le SARS-COV-2, 6 jours après l’entrée dans l’étude. Le rationnel pour le choix de ce critère, et encore moins pour le choix de la date du sixième jour, n’est pas décrit. C’est d’autant plus regrettable qu’on ne connaissait pas bien à l’époque les éventuelles relations entre durée de la positivité des PCR et devenir clinique des malades. En revanche, on supposait déjà qu’il existait assez fréquemment des faux-négatifs du test, ce qui pose évidemment problème pour une étude de ce type, qui repose donc sur un critère d’évaluation par essence imparfait. Le troisième point est qu’une étude d’observation destinée à évaluer un traitement doit définir des règles précises d’inclusion et d’exclusion. Ici, on lit notamment que les patients devaient avoir plus de 12 ans. Etonnamment, deux patients du groupe contrôle sont plus jeunes (10 ans !)…
De même, une fois les patients inclus, il faut éviter les exclusions secondaires qui sont souvent une manière d’orienter les résultats dans le sens qui convient à l’hypothèse des auteurs. Dans le cas présent, tous les patients du groupe contrôle sont restés dans l’étude, tandis que 6 patients du groupe traité (seulement 26 malades, à l’origine) ont été exclus secondairement : l’un d’entre eux est tout simplement mort à J3 ; trois ont été hospitalisés en réanimation (tous encore positifs avant leur transfert) ; un patient a dû arrêter le traitement qui n’était pas bien toléré ; il était encore positif à l’arrêt du traitement. Enfin, un patient a été perdu de vue, il était négatif avant la sortie de l’hôpital.
Enfin, il faut que les groupes comparés aient une taille suffisante pour pouvoir tirer des conclusions valides et il est nécessaire d’adopter des techniques statistiques d’ajustement pour pouvoir comparer des groupes qui ne le sont pas au départ : dans le cas présent, un groupe comprenait 20 patients et l’autre 16, et il y avait une différence de 15 ans de moyenne d’âge entre les deux groupes. En somme des petits groupes, pour lesquels une comparaison directe, non ajustée, n’est clairement pas appropriée.
Bref, une étude manquant vraiment de rigueur et qui ne pouvait apporter aucune conclusion raisonnable sur l’efficacité du traitement évalué. Une autre façon de voir les résultats, tout aussi critiquable, aurait été de dire que le traitement par hydroxychloroquine était particulièrement toxique : 5 patients sur 26 (19 %) ayant eu une évolution clinique défavorable ou une intolérance au traitement, tandis qu’aucun des 16 n’ayant pas reçu le traitement n’avait, apparemment, évolué défavorablement…

En résumé
Les études d’observation sont précieuses car elles permettent d’aller au-delà de la simple impression clinique. Elles sont cependant sujettes à une sorte de péché originel : elles ne peuvent jamais permettre d’affirmer formellement une relation de causalité, en raison de biais potentiels, tantôt évidents, tantôt cachés. Malgré cela, des techniques statistiques adaptées et un protocole d’étude rigoureux peuvent suggérer l’efficacité, la toxicité, ou la neutralité de tel ou tel type de traitement, et cela dans les conditions réelles d’utilisation, qui ne sont jamais exactement celles des études randomisées.
Nicolas Danchin,
HEGP, Paris
Les liens d’intérêt de l’auteur sont inscrits page 3.
En outre, l’auteur était membre du comité scientifique de l’étude NAXOS.
RÉFÉRENCES
1. Van Ganse E, Danchin N, Mahé I, Hanon O, Jacoud F, Nolin M, Dalon F, Lefevre C, Cotté FE, Gollety S, Falissard B, Belhassen M, Steg PG. Comparative Safety and Effectiveness of Oral Anticoagulants in Nonvalvular Atrial Fibrillation: The NAXOS Study. Stroke 2020; 51: 2066-75
2. Gautret P, Lagier JC, Parola P, Hoang VT, Meddeb L, Mailhe M, Doudier B, Courjon J, Giordanengo V, Vieira VE, Tissot Dupont H, Honoré S, Colson P, Chabrière E, La Scola B, Rolain JM, Brouqui P, Raoult D. Hydroxychloroquine and azithromycin as a treatment of COVID-19: results of an open-label non-randomized clinical trial. Int J Antimicrob Agents 2020; 56(1):105949.
